반응형

집합 A에 대한 관계 R은 특정 성질에 따라 나뉘어진다
4개의 성질들을 외우고
방향그래프로 보면서 이해하는게 더 쉬운거같다!
1. 반사관계 : 집합 A의 모든원소 x에 대해 xRx을 만족
A = {1,2,3,4}라고 할때
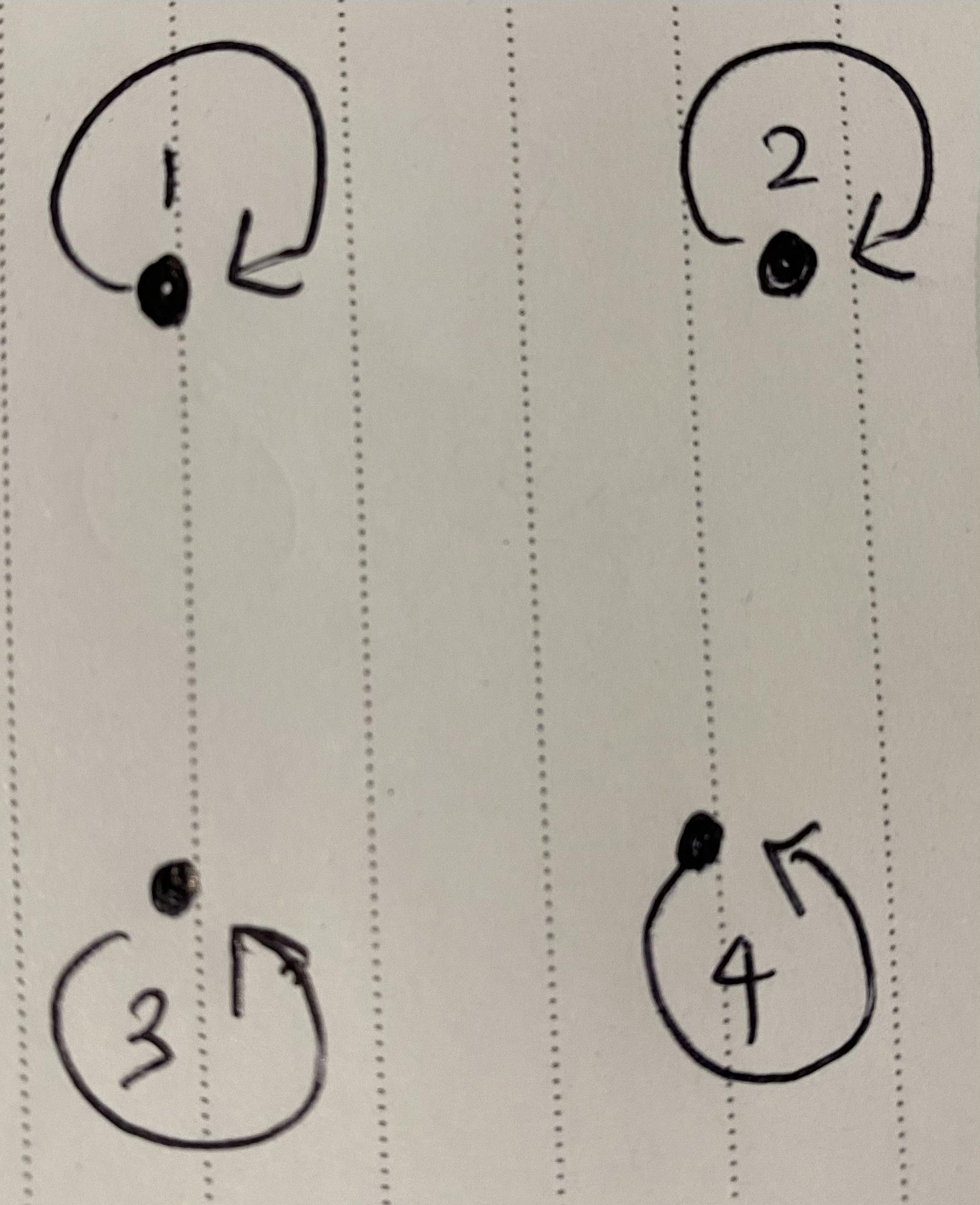
집합의 모든 원소가 xRx를 만족하기 때문에 반사관계이다
2. 대칭관계 : xRy 이면 yRx임을 만족
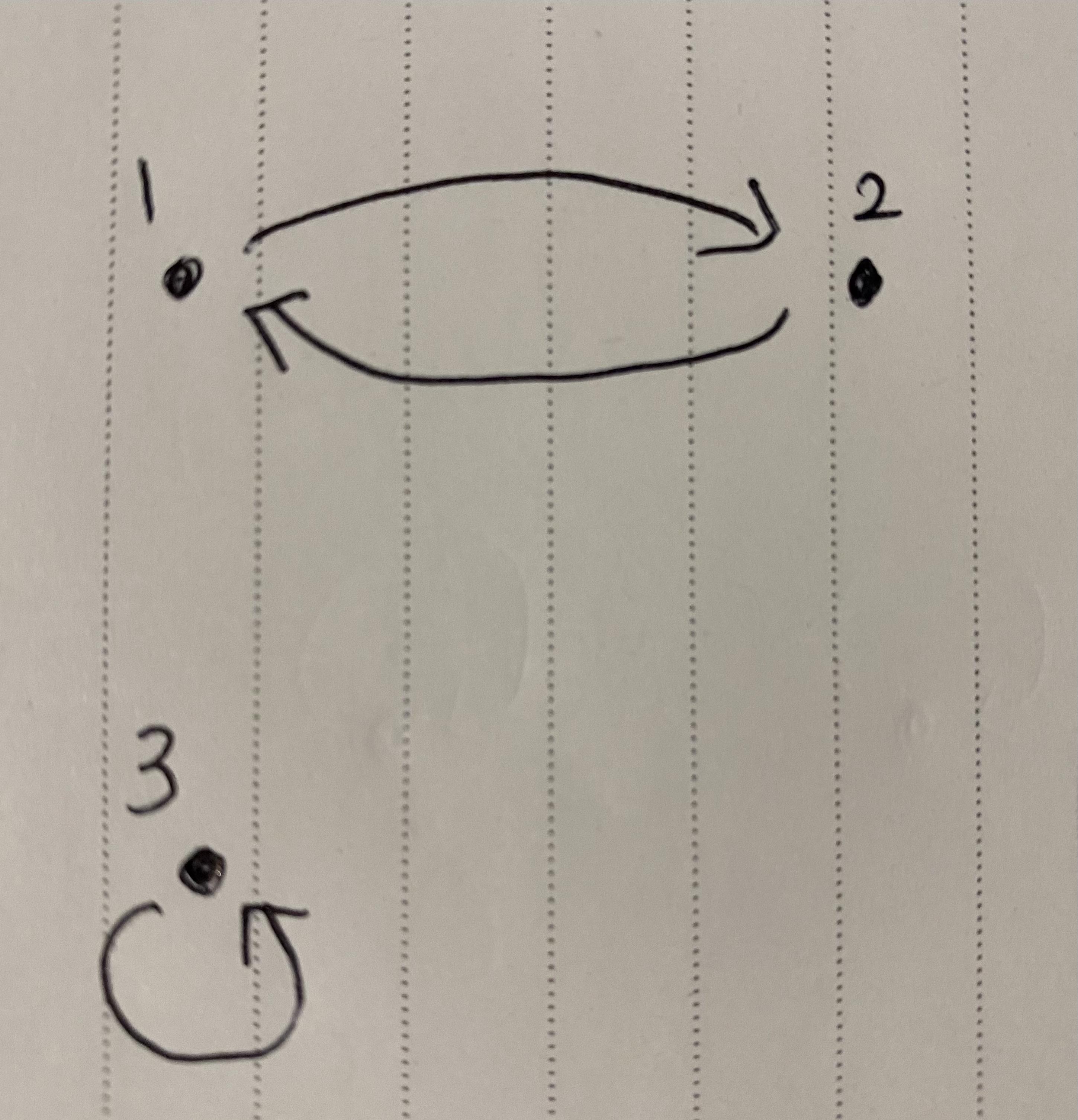
1R2 이면 2R1 이기 때문에 대칭관계이다. ( 3R3 또한 대칭)
반사관계와 달리
위 그림에서 원소 1,3이 대칭관계가 아닌데도 관계 R이 대칭관계가 되는이유는
p -> q 에서 p가 false 일때 항상 참이 되기 때문이다.
(xRy가 없(false)기 때문에 대칭관계는 참)
3. 반대칭관계 : xRy이고 yRx 일때 x=y를 만족
(대칭관계와 정반대개념이 아니다!)

반대칭 관계는 간단하게 xRx 외의 대칭관계가 존재하면 성립하지 않는 관계이다.
위의 관계에서 3R3 외의 대칭관계가 없기때문에 반대칭 관계이다.
대칭관계와 정반대 개념이 아닌것은
R = {(1,1),(2,2)} 만 있을때 반사관계와 반대칭관계가 동시에 성립하는것으로 증명할 수 있다.
(각각의 관계 성립 조건을 확인해보자)
4. 추이관계 : xRy 이고 yRz 일때 xRz을 만족

1R2이고 2R3 일때 1R3이 존재하기 떄문에 추이관계이다!

