반응형

단사,전사,전단사 함수
1. 단사함수
f: A->B에서 a1,a2 ∈ A에 대하여 f(a1)=f(a2)이면 x1 = x2일 경우 단사함수 라고한다 ( one - to -one function)
Ran(f) ⊆ B이다. (치역)
롤 랭크게임이랑 비슷하다. 집합 A의 원소들은 겹치는 챔프를 고를수 없다.

2. 전사함수
f: A->B에서 에서 B의 모든 원소 b에 대하여 f(a)=b가 성립되는 a ∈ A가 적어도 하나존재할때 전사함수라고한다. (onto function)
Ran(f)=B
B의 모든 원소가 화살에 맞아야 성립할 수 있다.

3. 전단사 함수
f:A->B에서 f가 전사인 동시에 단사인 함수 (one-to-one correspond function)
Ran(f) = B

여러가지 함수들
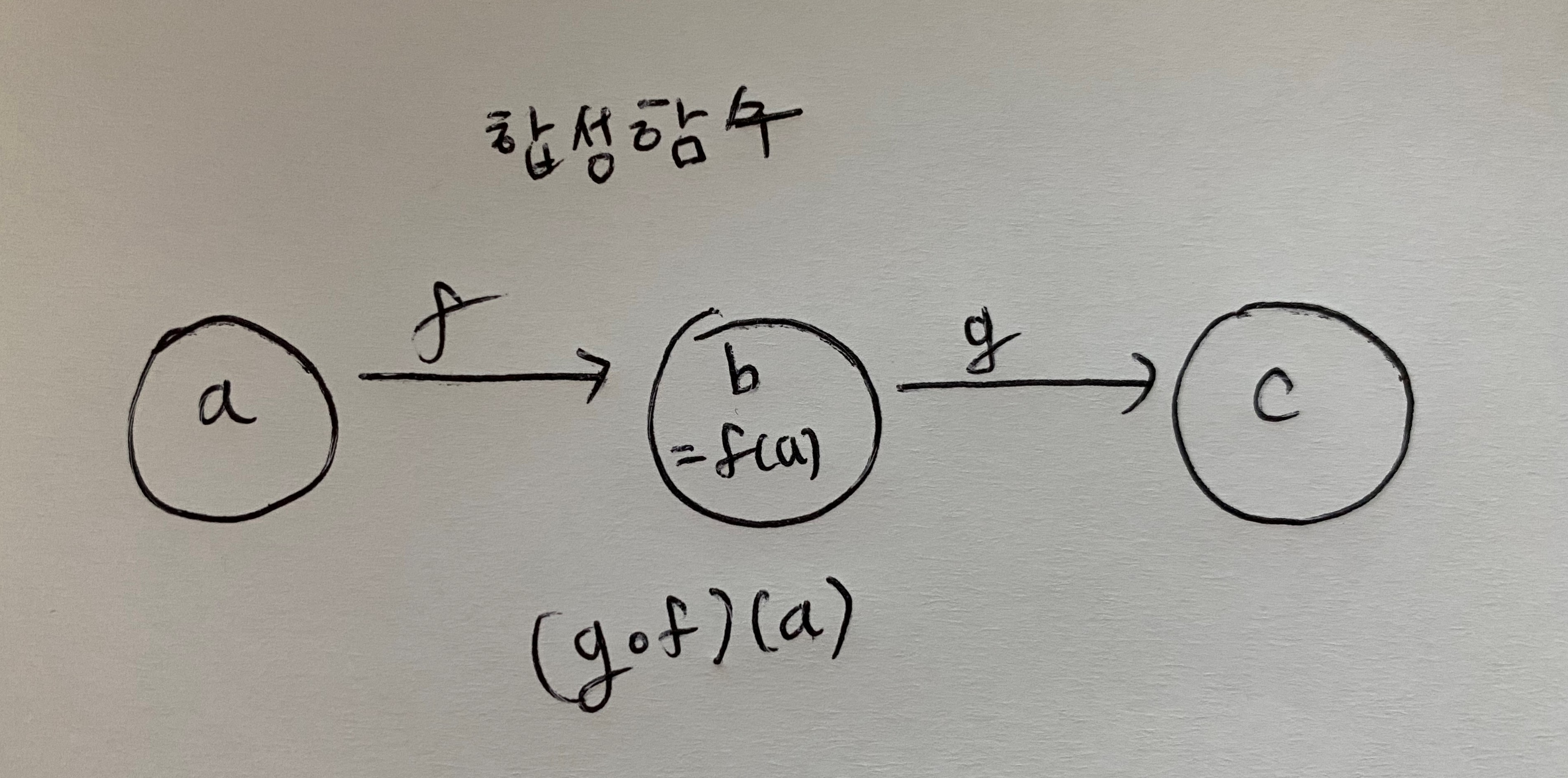
1. 함성함수
g ∘ f = {(a,c)| a∈A, b∈B, c∈C, f(a)=b, g(b)=c}
함수 f의 공역이 함수 g의 정의역이 될때 두 함수를 이어서 표현할수 있다.
2. 항등함수
f: A->A, f(a)=a 일때 함수 f를 항등함수라고한다
자기자신에게 대응하기때문에 전단사 함수이다.

3. 상수함수 (constant function)
f:A->B에서 집합 A의 모든 원소가 B의 한원소와 대응할때 함수 f를 상수함수 라고한다.
항상 같은 함수값을 가리키기 때문에 상수함수 라고한다.


